Menu

Coupling Conduction, Convection and Radiative Transfer in a Single Path-Space: Application to Infrared Rendering

Mégane Bati, Stéphane Blanco, Christophe Coustet, Vincent Eymet, Vincent Forest, Richard Fournier, Jacques Gautrais, Nicolas Mellado, Mathias Paulin, Benjamin Piaud

ACM Transactions on Graphics, 2023, 42 (4), ⟨10.1145/3592121⟩. ⟨hal-04090428⟩. Siggraph 2023

Abstract: In the past decades, Monte Carlo methods have shown their ability to solve PDEs, independently of the dimensionality of the integration domain and for different use-cases (e.g. light transport, geometry processing, physics simulation). Specifically, the path-space formulation of transport equations is a key ingredient to define tractable and scalable solvers, and we observe nowadays a strong interest in the definition of simulation systems based on Monte Carlo algorithms. We also observe that, when simulating combined physics (e.g. thermal rendering from a heat transfer simulation), there is a lack of coupled Monte Carlo algorithms allowing to solve all the physics at once, in the same path space, rather than combining several independent MC estimators, a combination that would make the global solver critically sensitive to the complexity of each simulation space.

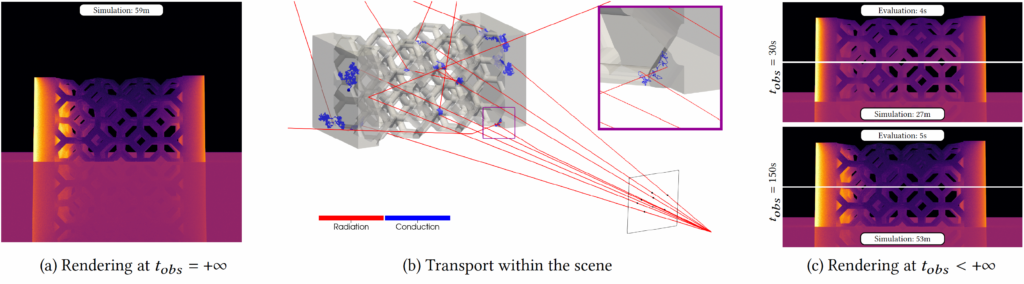
This brings to our proposal: a coupled, single path-space, Monte Carlo algorithm for efficient multi-physics problems solving. In this work, we combine our understanding and knowledge of Physics and Computer Graphics to demonstrate how to formulate and arrange different simulation spaces into a single path space. We define a tractable formalism for coupled heat transfer simulation using Monte Carlo, and we leverage the path-space construction to interactively compute multiple simulations with different conditions in the same scene, in terms of boundary conditions and observation time. We validate our proposal in the context of infrared rendering with different thermal simulation scenarios: e.g., room temperature simulation, visualization of heat paths within materials (detection of thermal bridges), heat diffusion capacity of thermal exchanger. We expect that our theoretical framework will foster collaboration and multidisciplinary studies. The perspectives this framework opens are detailed and we suggest a research agenda towards the resolution of coupled PDEs at the interface of Physics and Computer Graphics.

We propose a Monte Carlo approach to tackle multiple physics with a single algorithm, translating their coupling into a single path-space composed of randomly chained sub-paths for each physics. Application is exemplified with heat transfer. (a) An infrared image of a steady state thermal exchanger, with temperature imposed on the left and right walls. (b) Monte Carlo paths alternate between heat-transfer modes (here conduction and radiation). (c) A huge benefit is the fast production of transient simulations, at any time, using the information gathered in (a), i.e. from only one Monte Carlo run at steady state.

This work was supported by the ANR under grand No.: ANR-18-CE46-0012 (MCGRad: https://anr.fr/Project-ANR-18-CE46-0012).