 |
Maîtrise d'informatique - Module 18
|
 |
Maîtrise d'informatique - Module 18
|
Ce chapitre vise à rappeler un certain nombre de concepts mathématiques de base, dans les domaines de l'algèbre linéaire et de l'analyse. Il a pour but de "préparer le terrain", en vue de l'introduction de la transformation de Fourier qui sera faite dans le chapitre 2.
Dans ce paragraphe, plusieurs définitions de base d'algèbre linéaire vont être rappelées.
On appelle combinaison linéaire des vecteurs a1, a2, ..., an, toute somme de la forme suivante :
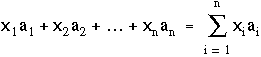
Dans cette somme finie (c'est-à-dire ne comportant qu'un nombre fini de termes), les coefficients x1, x2, ..., xn sont en général réels ou complexes.
On ne se préoccupera pas de donner la définition exacte d'un espace vectoriel, dans le cadre de ce cours. La propriété essentielle d'un espace vectoriel est la suivante : toute combinaison linéaire d'éléments (ou vecteurs) d'un espace vectoriel appartient à cet espace vectoriel. On dit qu'un espace vectoriel est stable par combinaison linéaire.
Exemples :
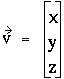
![]()
où la notation entre barres désigne le module de f(u). Nous retrouverons cet espace vectoriel à la fin de ce chapitre.
On appelle famille libre tout ensemble, non forcément
fini, d'éléments d'un espace vectoriel, soit ![]() ,
tel que, si une combinaison linéaire
,
tel que, si une combinaison linéaire ![]() de ces éléments est nulle (J doit nécessairement être
un ensemble d'indices de cardinal fini n), alors forcément tous
les coefficients x1, x2, ..., xn sont
nuls.
de ces éléments est nulle (J doit nécessairement être
un ensemble d'indices de cardinal fini n), alors forcément tous
les coefficients x1, x2, ..., xn sont
nuls.
On appelle famille génératrice d'un espace vectoriel, tout ensemble, non forcément fini, d'éléments de cet espace vectoriel, tel que tout élément de l'espace vectoriel est égal à une combinaison linéaire au moins des éléments de cet ensemble.
On appelle base d'un espace vectoriel toute famille de cet espace vectoriel qui est à la fois libre et génératrice.
On peut montrer que toutes les bases d'un même espace vectoriel possèdent le même nombre d'éléments. On appelle dimension d'un espace vectoriel le nombre d'éléments d'une base quelconque de cet espace vectoriel.
Exemples :
Dans ce paragraphe, nous allons introduire la fonction exponentielle en recherchant les solutions d'une équation différentielle. La fonction exponentielle est fondamentale en traitement du signal, et intervient en particulier dans la définition de la transformation de Fourier, comme nous le verrons au chapitre 2.
Soit l'équation différentielle suivante, dans laquelle l'inconnue est la fonction f(u), supposée dérivable :
![]() (1.1)
(1.1)
Cette équation doit être vérifiée par f(u), pour toute valeur de la variable réelle u. C'est une équation différentielle linéaire, à coefficients constants, du premier ordre de dérivation, homogène (c'est-à-dire à second membre nul). Sa caractéristique la plus intéressante est d'être linéaire, car cela implique que l'ensemble de ses solutions, soit E, est un espace vectoriel. Montrons en effet que, si f1(u) et f2(u) sont deux solutions quelconques de (1.1), et si x1 et x2 sont deux réels quelconques, alors (x1f1+x2f2)(u) est également solution :
![]()
Les deux parenthèses du membre droit étant nulles, on en déduit que (x1f1+x2f2)(u) est bien solution de (1.1).
Comme E est un espace vectoriel, résoudre (1.1) revient à chercher une base de E. Nous allons d'abord tenter de trouver une telle base parmi les fonctions monômes, qui constituent une famille libre de fonctions.
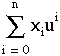
notation dans laquelle la valeur 0 de i correspond au terme constant du polynôme. Néanmoins, P est un espace vectoriel assez limité, car beaucoup de fonctions réelles d'une variable réelle ne sont pas polynômiales, comme par exemple cos, sin, ln, ...
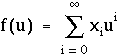
Cette écriture ne constitue pas une combinaison linéaire de monômes, car il s'agit d'une somme infinie, c'est-à-dire comportant un nombre infini de termes. En conséquence, une telle écriture n'a de sens que si elle est convergente (on dit aussi "sommable", ou "bornée"), et ceci pour tout réel u. On appelle ces fonctions les fonctions analytiques. On peut montrer qu'elles forment un espace vectoriel, noté A.
Remarques :
On souhaite trouver les solutions analytiques de l'équation (1.1). Soit une fonction analytique, définie par :
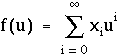 (1.2)
(1.2)
Sa dérivée s'écrit :
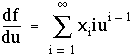
En faisant un changement d'indice, on réécrit cette somme :
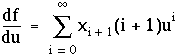
En combinant cette expression avec (1.2), on obtient :
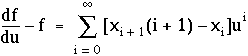
Une condition suffisante pour que cette expression s'annule est que, pour tout entier i :
![]()
On peut montrer que c'est également une condition nécessaire. Les coefficients xi sont donc déterminés de manière récurrente, à partir de la donnée de x0 :
![]()
Il est rappelé que 0! est égal à 1, par convention.
En réinjectant l'expression de xi trouvée précédemment dans (1.2), on obtient :
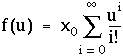 (1.3)
(1.3)
La somme apparaissant dans le second membre est-elle convergente, pour tout u réel ? On montre que oui, et on définit la fonction exponentielle exp(u), également notée eu, par cette somme :
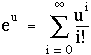 (1.4)
(1.4)
D'après (1.3), les solutions analytiques de (1.1) s'écrivent :
![]()
où x0 est un réel quelconque. L'intersection des espaces vectoriels E et A, qui est un espace vectoriel, admet donc comme base la fonction exponentielle, ce qui signifie que cet espace vectoriel est de dimension 1.
Signalons au passage que la résolution directe de l'équation (1.1), par la méthode de "séparation des variables", aurait donné très simplement le résultat précédent.
Par analogie avec (1.4), on définit la fonction exponentielle d'une variable imaginaire pure jv, où j2=-1, de la façon suivante :
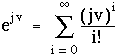
En séparant partie réelle et partie imaginaire, on obtient :
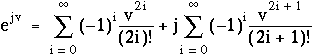
Les deux sommes apparaissant dans le second membre sont convergentes, pour tout réel v. On les appelle par définition cosinus et sinus de v, fonctions que l'on désigne respectivement par cos et sin, de sorte que :
![]() (1.5)
(1.5)
Avant de passer au cas d'une variable complexe, prouvons la propriété suivante de la fonction exponentielle, pour deux réels u et w quelconques :
![]()
En utilisant seulement la définition (1.4), cette propriété est relativement difficile à prouver. Il existe cependant une démonstration plus astucieuse. Supposons d'abord que w soit un réel fixé. La fonction eu+w est alors une fonction de la seule variable u, que l'on note par exemple fw(u). Sa dérivée est facile à calculer, en utilisant la formule bien connue de la dérivée de la composée de deux fonctions :
![]()
Ceci signifie que fw(u) est solution de (1.1). Comme c'est une fonction analytique, on peut affirmer, d'après l'étude faite dans le paragraphe précédent, qu'il existe une fonction x0(w), ne dépendant pas de u, telle que :
![]()
De la même façon, on montre l'existence d'une fonction x1(u), telle que :
![]()
En égalant les seconds membres de ces deux égalités, on déduit qu'il existe une constante réelle x2, telle que :
![]() et
et
![]()
D'où l'égalité suivante :
![]()
En annulant simultanément u et w, et sachant que la fonction exponentielle vaut 1 en 0, on en déduit que x2 vaut 1. On obtient donc bien la propriété annoncée plus haut, c'est-à-dire :
![]() (1.6)
(1.6)
Cette propriété se généralise facilement au cas où u ou w est imaginaire pur. Nous pouvons maintenant donner l'expression de la fonction exponentielle d'une variable complexe quelconque.
Dans le cas d'une variable complexe quelconque, on pourrait encore définir la fonction exponentielle par analogie avec (1.4), mais cela risquerait d'être un peu compliqué. Mieux vaut utiliser la propriété (1.6) vue précédemment, qui permet d'écrire, si u et v sont deux réels quelconques :
![]()
En utilisant l'égalité (1.5), on obtient :
![]() (1.7)
(1.7)
Dans ce paragraphe, nous allons faire un petit récapitulatif sur les notions qui ont été abordées jusqu'à présent et, en particulier, nous allons revenir sur les différents espaces vectoriels de fonctions qui ont déjà été introduits.
A la lumière du paragraphe précédent, on peut distinguer les trois familles de fonctions exponentielles suivantes :
Cette famille ne présente pas d'intérêt particulier en traitement du signal.
Cette famille de fonctions exponentielles s'appelle la famille de Fourier (Joseph Fourier : 1768-1830). Elle est fondamentale dans la définition de la transformation de Fourier, qui sera introduite dans le chapitre 2.
Cette famille de fonctions exponentielles s'appelle la famille de Laplace (Pierre de Laplace : 1749-1827). Elle est fondamentale dans la définition de la transformation de Laplace, qui ne sera pas introduite dans le cadre de ce cours.
On peut remarquer que la famille de Laplace contient les deux autres familles. Nous allons montrer que la famille de Laplace est une famille libre. Si tel est le cas, toute sous-famille d'une famille libre étant libre (cela est facile à vérifier), on aura aussi montré que les deux autres familles sont libres.
Soit donc une combinaison linéaire de n fonctions de Laplace distinctes :
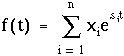
Supposons que cette fonction soit nulle, quel que soit t réel. En ce cas, toutes les dérivées successives de f(t) sont également nulles. Donc en particulier, pour tout entier k compris entre 0 et n-1 :
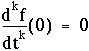
c'est-à-dire :
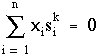
Ceci constitue un système de n équations linéaires à n inconnues, qui sont les coefficients complexes xi. Le déterminant de ce système s'écrit :
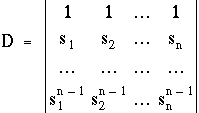
C'est un déterminant de Van der Monde, bien connu en algèbre linéaire, dont on peut montrer qu'il vaut aussi :
![]()
où l (il s'agit de la lettre l et non pas du chiffre 1) et m sont compris entre 1 et n. Or, on a fait l'hypothèse que tous les complexes si étaient distincts, donc cette expression est non nulle. Par conséquent, le système d'équations précédent est un système de Cramer, n'admettant que la solution évidente suivante :
![]()
Ceci prouve bien le résultat annoncé, c'est-à-dire que la famille de Laplace est une famille libre.
Dorénavant, nous ne nous intéresserons plus qu'à la famille de Fourier.
Faisons un raisonnement par analogie :
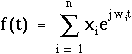
Cet espace vectoriel est très limité et ne présente aucun intérêt particulier. Cependant, de même que pour P, on peut construire un autre espace vectoriel à partir de la famille de Fourier, que l'on note T, en étendant les combinaisons linéaires aux intégrales sur R, convergentes. Les fonctions f(t) contenues dans T s'écrivent donc sous la forme suivante :
![]() (1.8)
(1.8)
Etant donné que la somme a été transformée en intégrale, les coefficients xi ont été transformés en une fonction x(w). Le choix d'une fonction x(w) est limité par la contrainte suivante : l'intégrale doit être convergente, quel que soit le réel t. Comme nous le verrons dans le chapitre 2, T est l'espace vectoriel des fonctions complexes d'une variable réelle admettant une transformée de Fourier, ce qui suffit à montrer que T est beaucoup plus intéressant que F.
On peut faire un récapitulatif de ces quatre espaces vectoriels de fonctions, sous la forme du tableau suivant :
| espace
vectoriel |
construit à
partir de la |
ayant pour
base la |
ayant pour éléments
les fonctions du type |
appelées |
| P | famille des
monômes |
famille des
monômes |
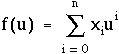 |
fonctions
polynômes |
| A | famille des
monômes |
? | 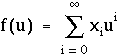
si cette somme est convergente, quel que soit le réel u |
fonctions
analytiques |
| F | famille de
Fourier |
famille de
Fourier |
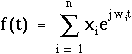 |
? |
| T | famille de
Fourier |
? | si cette intégrale est convergente, quel que soit le réel t |
"fonctions admettant
une transformée de Fourier" |
Remarques :
![]()