
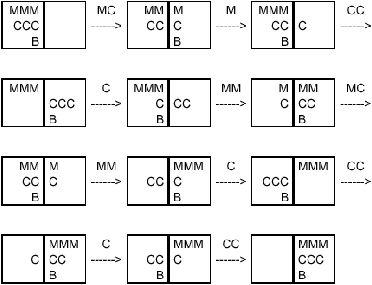
| Les ordis c'est bon pour | Les gens sont meilleurs pour |
| l'arithmétique | perception, vision, parole, etc. |
| manipuler des chaînes de caractères | l'action |
| les tâches répétitives | comprendre et produire des phrases en langage naturel |
| faire ce qu'on leur dit | apprendre par exemples, observation,... |
| le raisonnement de sens commun | |
| les jeux | |
| les mathématiques et la logique formelle | |
| la conception et l'analyse (ingénierie, diagnostic médical, architecture, planification, etc) |
| raisonnement | démonstration automatique, planification |
| jeux | |
| apprentissage | |
| langage | interfaces, recherche d'informations |
| vision | extraction, reconnaissances de formes, surveillance |
| diagnostic | pannes, diagnostic médical |
| base de données | base de connaissances |



| T(n) = O(f(n)) ssi |
|
|
= cte |
| T(n) / n | 10 | 20 | 30 | 40 | 50 | 60 |
| n | 10µs | 20 µs | 30 µs | 40 µs | 50 µs | 60 µs |
| log n | 1µs | 1.3 µs | 1.5 µs | 1.6 µs | 1.7 µs | 1.8 µs |
| n log n | 10µs | 26 µs | 44 µs | 64 µs | 85 µs | 107 µs |
| n2 | 100µs | 400 µs | 900 µs | 1.6ms | 2.5 ms | 3.5 ms |
| n3 | 1ms | 8 ms | 27 ms | 64 ms | 125 ms | 216 ms |
| n5 | 0.1s | 3.2s | 24.3s | 1.7 mn | 5.2 mn | 13 mn |
| 2n | 1ms | 1s | 18mn | 13jours | 36 ans | 366 siècles |
| 3n | 59ms | 58 mn | 6 mn | 3855 siècles | 2.108 siècles | 1.3.1013 siècles |
| T(n) | aujourd'hui | si 100 fois plus vite | si 1000 fois plus vite |
| n | N | 100N | 1000N |
| n2 | N | 10N | 32N |
| n3 | N | 4.6N | 10N |
| n5 | N | 2.5N | 4N |
| 2n | N | N + 7 | N + 10 |
| 3n | N | N + 4 | N + 6 |


...the key to happiness is to lower your expectations to the point where they are already met.
L'ordre du graphe est son nombre de noeuds.
|
d(x)= 2 |A| |
|
d+(x)= |
|
d-(x)= |A| |

Complexité ? en espace O(n+m)

Théorème : si G est connexe tous les sommets seront marqués par l'agorithme et toutes les arêtes seront explorées au moins une fois.
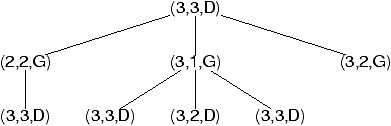
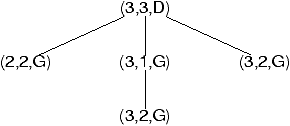

| h*(n)=min |
|
k(n,γ) |
| 1 | 3 | 4 |
| 8 | 2 | |
| 7 | 6 | 5 |

This document was translated from LATEX by HEVEA.