 |
Maîtrise d'informatique - Module 11
|
 |
Maîtrise d'informatique - Module 11
|
Nous appelons "stéréovision" la reconnaissance du relief à partir de plusieurs images d'une même scène, vue sous différents angles.
Dans ce cours, nous nous limitons à la stéréovision binoculaire, donc à des paires d'images, formées d'une image "gauche" et d'une image "droite" (remarquer la similarité avec la vision humaine).
La stéréovision, comme nous l'avons déjà mentionné au chapitre 2, s'effectue en trois étapes successives :
La phase la plus difficile est la phase 2. C'est aussi celle qui varie le plus d'une méthode à l'autre. Les phases 1 et 3 sont purement géométriques, contrairement à la phase 2 qui utilise les niveaux de gris Ei,j des deux images.
Dans ce chapitre, nous allons simuler, dans un cas particulièrement simple, chacune de ces trois phases.
Ce cas survient lorsqu'on n'utilise qu'une caméra, ce qui impose à la scène d'être statique. L'intérêt de n'utiliser qu'une caméra est que les paramètres de la caméra sont les mêmes entre les images gauche et droite. En d'autres termes, la phase de calibrage est nettement simplifiée.
Dans le cas général, par contre, ces paramètres diffèrent, et doivent être déterminés les uns par rapport aux autres.
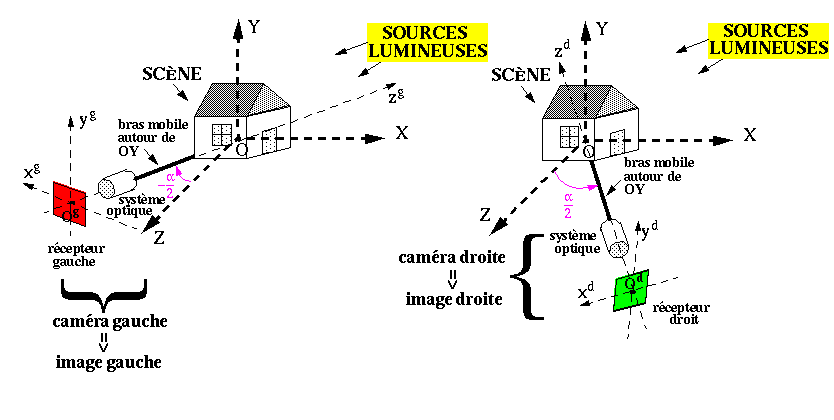
À partir d'une paire d'images numériques stéréoscopiques, on souhaite connaître Z pour chaque point de la scène.
Si l'image est nette, la correspondance entre les points objets et les pixels des images peut être considérée comme la succession de :
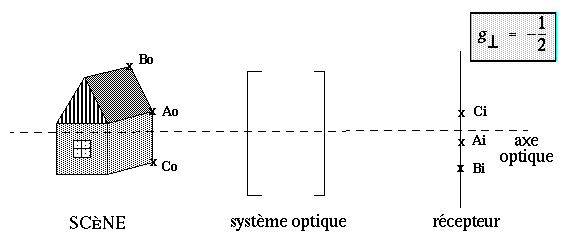
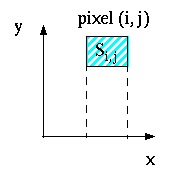
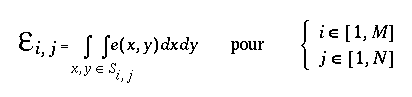
Il va être très simple ici.
Soit un point objet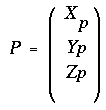 visible
sur les deux images.
visible
sur les deux images.
On cherche 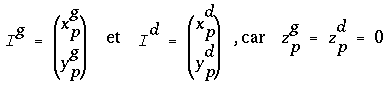 .
.
Une remarque évidente est que :
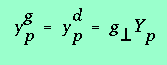 (3.1)
(voir
plus loin l'intérêt de cette formule)
(3.1)
(voir
plus loin l'intérêt de cette formule)
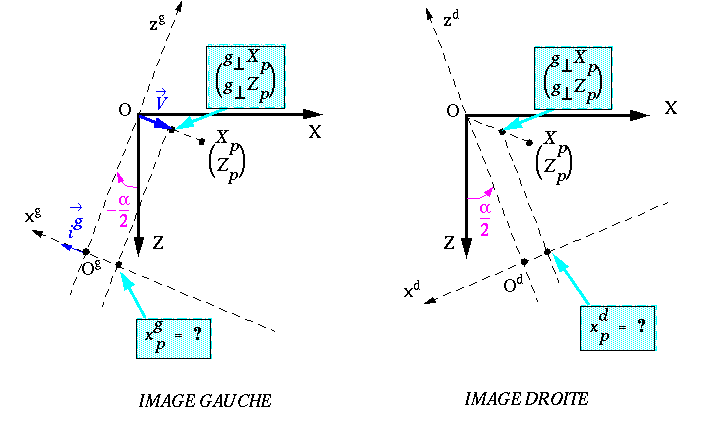
Si on sait calculer xgp , on aura
xdp en remplaçant - ![]() par
par
![]() .
.
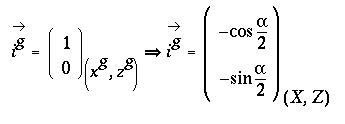
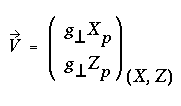
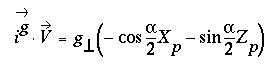
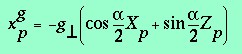 (3.2)
(3.2)
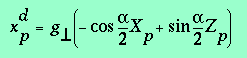 (3.2 bis)
(3.2 bis)
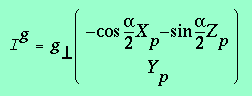 (3.3)
(3.3)
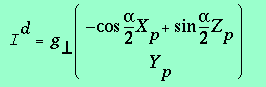 (3.3 bis)
(3.3 bis)
Calibrer consiste à déterminer
les coefficients permettant de calculer Ig
et Id pour tout
point objet 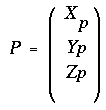 .
.
D'après les relations (3.3) et (3.3 bis), il y a dans notre cas
deux paramètres à déterminer :![]() et
et
![]() .
.
D'après (3.3) et (3.3 bis),![]() est
un facteur d'échelle, dont on observe
toujours la présence en stéréovision. C'est même
le seul paramètre de calibrage qui apparaisse dans tous les cas.
est
un facteur d'échelle, dont on observe
toujours la présence en stéréovision. C'est même
le seul paramètre de calibrage qui apparaisse dans tous les cas.
L'angle ![]() ne
dépend pas des caractéristiques internes de la caméra.
Pour cette raison, on dit que
ne
dépend pas des caractéristiques internes de la caméra.
Pour cette raison, on dit que ![]() est
un paramètre "extrinsèque"
de calibrage.
est
un paramètre "extrinsèque"
de calibrage.
Soit un point objet pour lequel on connaît :
On a donc :
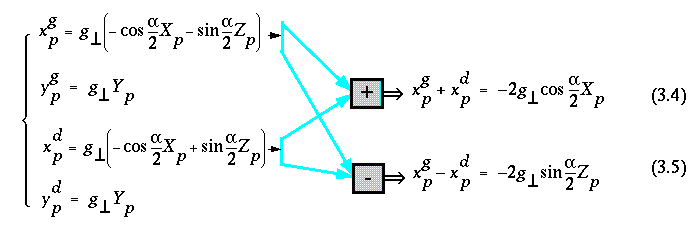
Le produit du membre gauche de (3.4) par le membre droit de (3.5) est
égal au produit du membre droit de (3.4) par le membre gauche de
(3.5), ce qui donne, en divisant à gauche et à droite par
-2![]() :
:
Cette équation se réécrit :
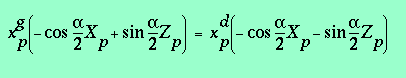 (3.6 bis)
(3.6 bis)
Dans (3.6) ou (3.6 bis), seul![]() est
inconnu.
est
inconnu.
Si![]() et
et![]() ,
alors, d'après la remarque précédente et les équations
(3.4) et (3.5), on voit que
,
alors, d'après la remarque précédente et les équations
(3.4) et (3.5), on voit que ![]() et
et ![]() .
On peut donc, dans ce cas, transformer (3.6) de la manière suivante :
.
On peut donc, dans ce cas, transformer (3.6) de la manière suivante :
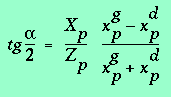 (3.7)
(3.7)
Résolution graphique de (3.7) :
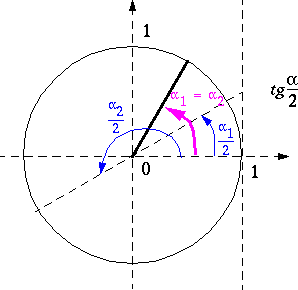
Cette résolution graphique montre qu'il y a deux solutions en
![]() :
:
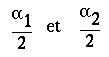 .
Mais, comme
.
Mais, comme 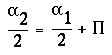 ,
il est clair que les deux angles
,
il est clair que les deux angles ![]() sont
égaux modulo
sont
égaux modulo![]() ,
c'est-à-dire qu'il y a une solution unique
,
c'est-à-dire qu'il y a une solution unique ![]() à (3.7), donnée par exemple par :
à (3.7), donnée par exemple par :
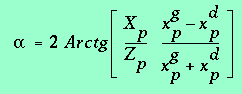 (3.8)
(3.8)
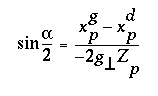
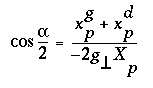
L'appariement ou "mise en correspondance" est la phase du traitement la plus difficile, car elle n'est pas purement géométrique. Cette phase fait appel aux niveaux de gris des deux images, contrairement aux phases 1 et 3, dans lesquelles on n'a jamais à utiliser les niveaux de gris Egi,j et Edk,l .
Nous allons commencer par comparer les niveaux de gris de deux pixels appariés.
On dit que deux pixels Igi,j et Idk,l sont appariés s'ils correspondent au même point physique P de la scène. Pour trouver de telles paires à partir de la donnée de deux images, on ne peut que chercher une similarité entre les niveaux de gris Egi,j et Edk,l correspondant à ces deux pixels :
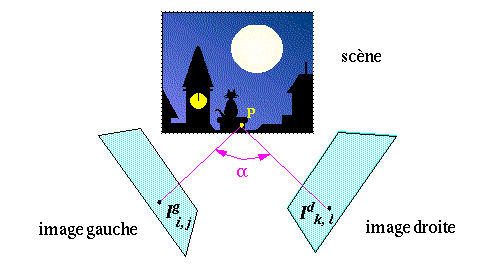
En fait, P ne réémet pas la même
énergie lumineuse dans toutes les directions, ce qui signifie que
Egi,j et Edk,l
ne sont pas égaux. On voit aussi que si![]() diminue,
les valeurs Egi,j et
Edk,l se rapprochent.
diminue,
les valeurs Egi,j et
Edk,l se rapprochent.
De toutes façons, on aura beaucoup de paires erronées si on se contente d'apparier un pixel Igi,j avec le pixel Idk,l qui a le niveau de gris Edk,l le plus proche de Egi,j .
Pour cette raison, on va comparer non pas un pixel
de l'image gauche avec un pixel de l'image droite, mais un pixel de l'image
gauche et son voisinage, avec un pixel de l'image droite et son voisinage.
C'est ce qu'on appelle la "corrélation".
Un pixel Igi,j de l'image gauche et un pixel Idk,l de l'image droite sont corrélés si les niveaux de gris ont des valeurs similaires au voisinage de ces deux pixels.
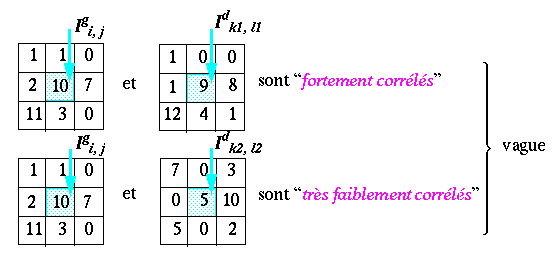
On souhaite pouvoir mesurer numériquement la corrélation entre deux pixels et leurs voisinages.
On peut chercher la corrélation entre deux pixels et leurs voisinages avec une taille de voisinage plus ou moins importante. On appelle ce voisinage la "fenêtre de corrélation".
On impose :
Cas le plus courant : fenêtre carrée centrée sur le pixel à apparier.

Il existe différentes méthodes pour mesurer numériquement la corrélation. La plus élémentaire est la mesure de corrélation euclidienne. Avec une fenêtre de corrélation 3 x 3, elle s'écrit :
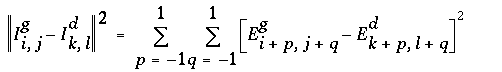
Avec l'exemple précédent :
![]()
=> pixels "fortement corrélés".
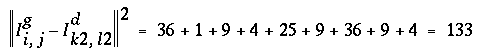
=> pixels "très faiblement corrélés".
Plus la mesure de corrélation euclidienne entre deux pixels et leurs voisinages est faible, plus ces pixels sont corrélés. Cela nous procure une méthode d'appariement.
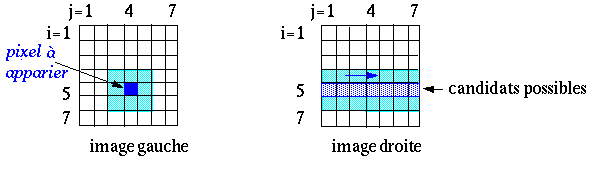
En fait, on se limite aux pixels pour lesquels la fenêtre de corrélation est entièrement contenue dans l'image. Cela élimine les candidats situés sur les bords.
Soit Igi,j un pixel de l'image gauche tel que la fenêtre de corrélation soit contenue dans l'image gauche. On cherche à apparier Igi,j. Les candidats sont les pixels Idi,l pour lesquels la fenêtre de corrélation est contenue dans l'image droite. On apparie Igi,j avec le pixel Idi,l pour lequel la mesure de corrélation euclidienne est minimale.
On a privilégié les pixels de l'image gauche sans raison. On peut donc réaliser la même opération pour les pixels de l'image droite. Si Igi,j a été apparié avec le pixel Idi,l , il se peut très bien que lors de l'opération inverse, Idi,l ne soit pas apparié avec Igi,j.
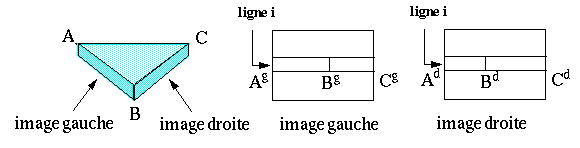
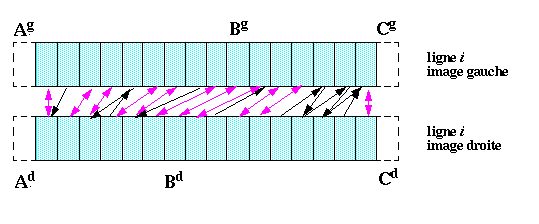
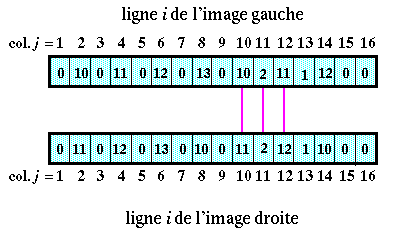
Chaque simple flèche noire désigne un appariement unilatéral, c'est-à-dire n'ayant pas débouché sur la formation d'une paire.
Les doubles flèches roses indiquent les paires formées d'un pixel de l'image gauche et d'un pixel de l'image droite, c'est-à-dire les paires apparaissant dans les deux appariements : ces paires vérifient ce qu'on appelle la "contrainte d'unicité".
Dans notre exemple, après application de la contrainte d'unicité, il ne reste plus que 11 paires (sur les 16 possibles).
Cette méthode d'appariement consiste à mettre en bijection nb pixels de l'image gauche (nb < N x M) avec nb pixels de l'image droite.
Un certain nombre de pixels restent non appariés, en particulier sur les bords. Cela n'est pas un problème, et nous verrons plus loin comment traiter ces pixels non appariés.
Un problème plus important est celui des appariements erronés, que nous allons évoquer dans le paragraphe suivant.
Avec la méthode que nous venons de voir, il est possible de traiter un couple de deux images quelconques :
=> couples de pixels appariés ????!!!!!
Même si on reste dans le cadre qui est le nôtre :
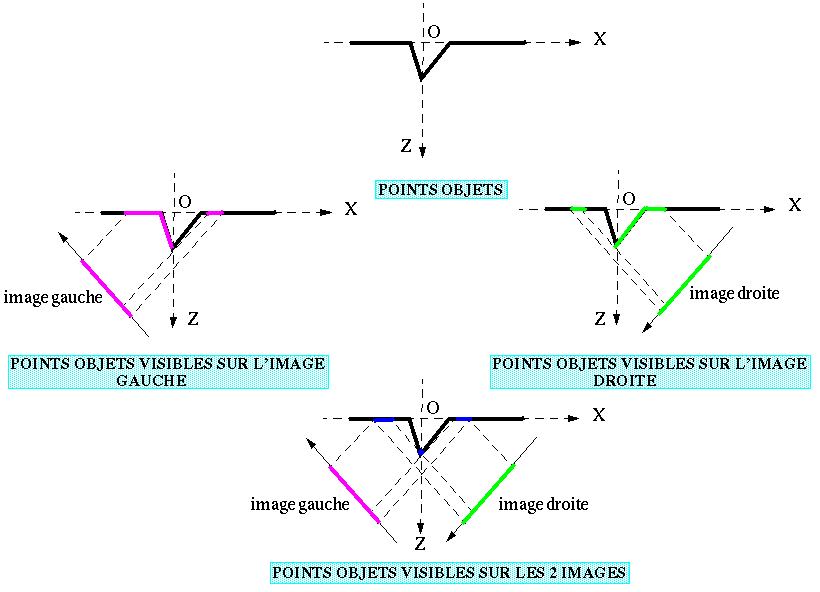
Il se peut très bien qu'un pixel correspondant à une des zones non visibles sur une des images ait été apparié. Il faut éliminer si possible un tel appariement, puisqu'il est forcément erroné.
Pour ce faire, nous introduisons un seuil S, et considérons que deux niveaux de gris Egi,j et Edi,l sont "proches" si et seulement si :
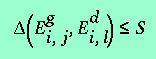 (3.9)
(3.9)
avec :
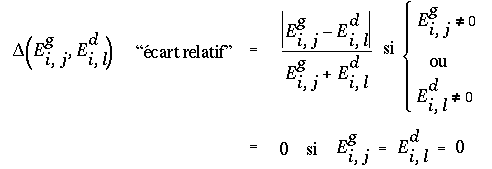

Comme la similarité entre deux pixels est jugée sur les voisinages de ces deux pixels, on va considérer que deux pixels (Igi,j , Idi,l ) forment une paire acceptable si (avec une fenêtre 3 x 3) :
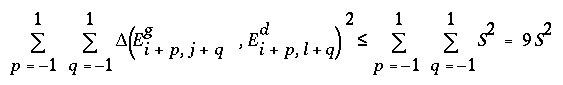
Il est possible de montrer qu'une condition suffisante pour que cette inégalité soit vérifiée s'écrit :
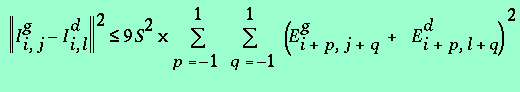 (3.10)
(3.10)
Les paires de pixels ne vérifiant pas cette égalité sont rejetées car trop suspectes. Ceci revient à imposer une contrainte de seuil.
Les trois contraintes que nous avons citées (épipolaire, d'unicité et de seuil) fournissent un ensemble de paires de pixels (Igi,j , Idi,l ) assez bon en général.
Il subsistera des erreurs dans le cas d'un motif périodique ou presque périodique.
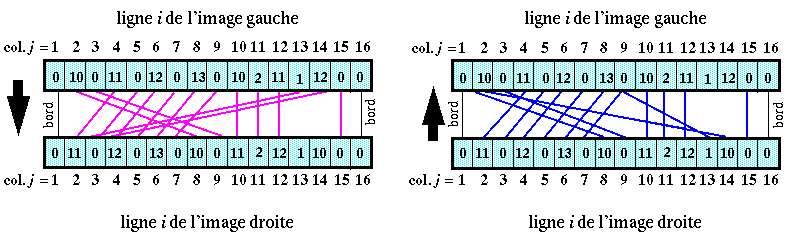
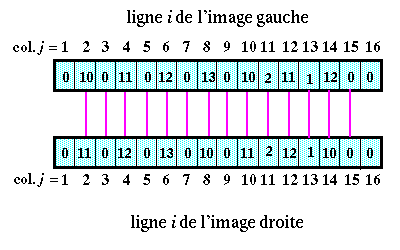
Sur le schéma précédent, le tableau de gauche correspond à la phase d'appariement des pixels de l'image gauche et le tableau de droite correspond à la phase d'appariement des pixels de l'image droite.
En appliquant les contraintes d'unicité et de seuil (avec S = 1), il ne reste que les 11 paires suivantes :
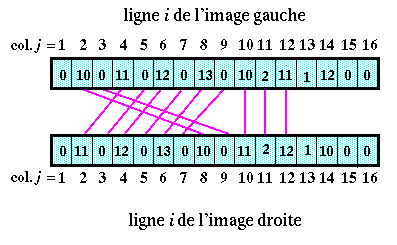
Or, on aurait plutôt tendance à penser que deux pixels formant une paire ont des numéros de colonnes identiques :
Il existe deux améliorations possibles à la méthode d'appariement décrite dans les paragraphes précédents :
Soit (Igi,j1, Idi,l1 ) et (Igi,j2, Idi,l 2) deux paires de pixels, vérifiant les trois contraintes citées précédemment (épipolaire, d'unicité et de seuil).
On impose en plus au produit (j2 - j1) x (l2 - l1) d'être supérieur ou égal à 0. Considérons l'exemple suivant :
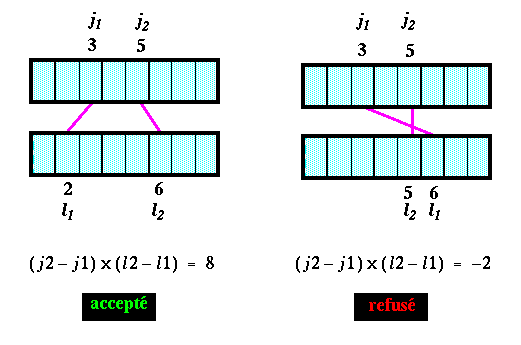
Si un pixel Igi,j1 est à gauche d'un pixel Igi,j2 sur l'image gauche, alors Idi,l1 doit être à gauche de Idi,l 2 sur l'image droite : c'est la contrainte d'ordre.
Dans l'exemple 2, la figure de droite présente deux paires qui ne vérifient pas cette contrainte.
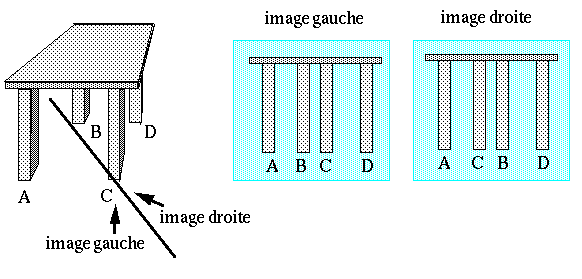
Dans la pratique, on cherchera à respecter cette contrainte en éliminant un minimum de paires. Dans l'exemple 1, il suffit d'enlever 2 paires pour respecter la contrainte d'ordre : (Igi,2 , Idi,8) et (Igi,3 , Idi,9). Mais cela ne change pas les appariements erronés. Que faire ?
Pour chaque pixel à apparier, on trace une courbe avec, en abscisse, les indices de colonnes des candidats et, en ordonnée, les mesures de corrélation qui leur correspondent.
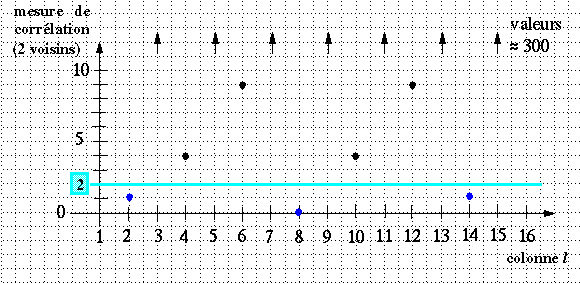
Deux attitudes sont possibles :
On obtiendra, avec l'exemple 1 (S' = 2) :
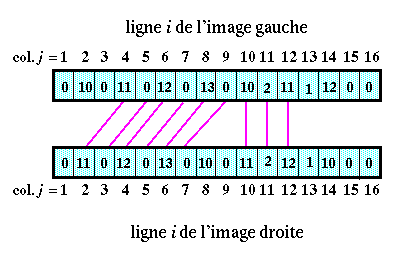
Changeons le seuil : les candidats retenus sont maintenant ceux pour lesquels la corrélation est inférieure ou égale à S' = 10.
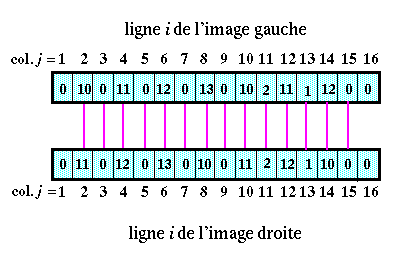
Au maximum, on peut réaliser 14 appariements (on ne pourrait pas en réaliser plus), qui sont tous exacts qui plus est !
Passons maintenant à la phase 3 de triangulation, la plus facile.
On suppose que :
Soit une paire de pixels appariés (Igi,j, Idi,l ). Le point P= (Xp,Yp,Zp) correspondant à cette paire vérifie les trois équations suivantes :
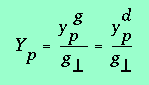 (3.11)
(3.11)
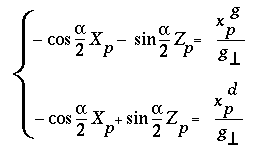
Les deux dernières équations constituent un système linéaire de deux équations à deux inconnues : Xpet Zp. Calculons son déterminant :
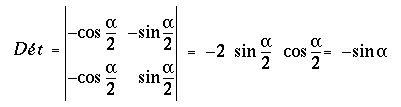
Comme ![]() et
et
![]() ,
il s'ensuit que
,
il s'ensuit que ![]() ,
donc que le système est un système de Cramer :
,
donc que le système est un système de Cramer :
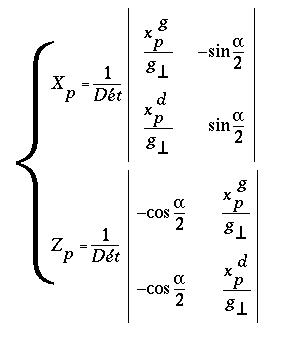
soit encore :
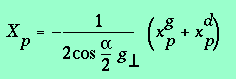 (3.12)
(3.12)
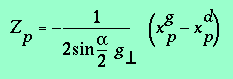 (3.13)
(3.13)
Dans (3.13) apparaît la différence :
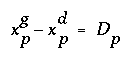 appelée
disparité d'un couple de pixels.
appelée
disparité d'un couple de pixels.
On voit que l'altitude d'un point P est proportionnelle
à la disparité du couple de pixels qui lui est associé.