 |
Maîtrise d'informatique - Module 18
|
 |
Maîtrise d'informatique - Module 18
|
L'objet essentiel de ce chapitre est d'introduire le moyen de calculer des transformées de Fourier à l'aide de l'outil informatique.
Les calculs de transformées de Fourier "à la main" doivent être abandonnés pour deux raisons :
Notons quand même qu'il existe, en "optique de Fourier", un système permettant de calculer la transformée de Fourier d'un signal bidimensionnel quelconque. Ce moyen constitue un "calculateur analogique".
Contrairement aux idées reçues, l'outil informatique peut constituer un calculateur analogique. Il s'agit alors de ce qu'on appelle le calcul formel. A l'aide de certains logiciels, qui autorisent le calcul de l'intégrale d'une fonction entre deux bornes, on peut calculer la transformée de Fourier d'une fonction d'expression analytique connue.
Exemple :
On désire calculer, à l'aide d'un logiciel de calcul formel,
la transformée de Fourier de la fonction "fenêtre"
déjà vue au chapitre 2. Comme un tel logiciel sait calculer
l'intégrale d'une fonction entre deux bornes, et que la fonction
"fenêtre" est nulle en dehors de l'intervalle [-1,1], il
suffit d'intégrer la fonction ![]() entre
les bornes -1 et 1, et le logiciel fournira comme résultat :
entre
les bornes -1 et 1, et le logiciel fournira comme résultat :
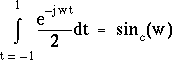
qui est bien la transformée de Fourier de la fonction "fenêtre".
Malheureusement, le calcul formel ne permet pas, lui non plus, de calculer la transformée de Fourier d'un signal réel.
Il s'agit dans ce cas de ce qu'on appelle le calcul numérique. L'intérêt du calcul numérique par rapport au calcul formel est qu'il permet de traiter tous les signaux, y compris les signaux réels. En revanche, le calcul numérique présente le défaut de faire perdre de l'information, et ceci à cause de deux phénomènes distincts et qu'il ne faut pas confondre :
Nous allons détailler successivement chacun de ces deux phénomènes.
Soit par exemple le signal analogique f(t) suivant :
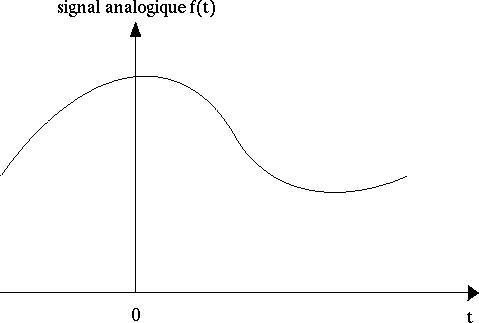
La discrétisation de ce signal revient à n'en garder qu'un certain nombre de valeurs (..., f-1, f0, f1, ...) correspondant aux valeurs (..., t-1, t0, t1, ...) de la variable t :
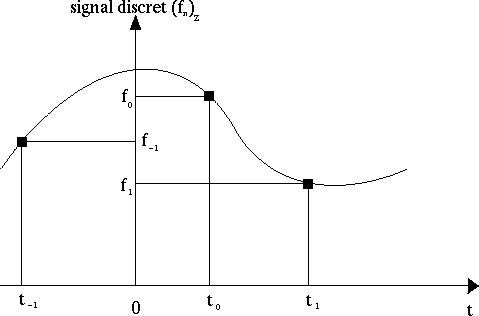
On ne dispose donc plus, après discrétisation, que d'une suite (fn)Z, où Z désigne l'ensemble des entiers relatifs. On appelle cette suite un signal discret associé au signal analogique f(t).
Dans la quasi-totalité des cas, l'échantillonnage est périodique, c'est-à-dire que ... = t0 - t-1 = t1 - t0 = ... = Te, valeur qu'on appelle la période d'échantillonnage. On définit aussi la pulsation d'échantillonnage par :
![]()
Un problème majeur en traitement du signal est le choix de cette pulsation d'échantillonnage we :
Nous verrons un peu plus loin qu'il existe un critère optimal pour choisir cette pulsation, qui s'appelle le "critère de Shannon".
La quantification est une opération qui modifie légèrement les valeurs du signal discret précédent. Ceci vient du fait qu'en informatique, les supports d'information ne sont pas analogiques mais binaires, et que donc toute valeur réelle ne peut pas être mémorisée. On peut par exemple représenter ce phénomène par le schéma suivant :
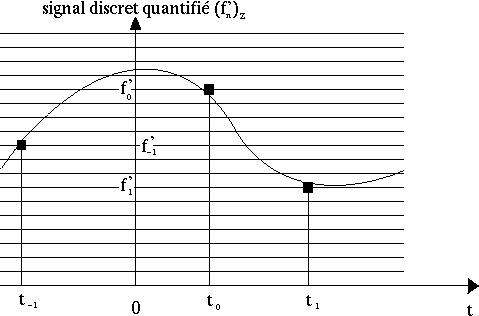
Sur ce schéma, les traits horizontaux représentent l'ensemble des valeurs possibles pour le signal.
On obtient donc, après quantification, une suite (f'n)Z
telle que, pour tout entier n, ![]() .
.
Remarques :
Dans toute la suite de ce cours, nous ne prendrons plus en compte que la discrétisation, et nous ne parlerons donc pas du moyen de tenir compte de l'erreur introduite par la quantification.
On a vu qu'il était très simple de passer d'un signal analogique f(t) au signal discret correspondant (fn)Z, pourvu qu'une pulsation d'échantillonnage we ait été choisie. L'opération inverse est-elle réalisable ?
Soit f(t) le signal analogique de départ et Te la période d'échantillonnage. Le signal discret est la suite (fn)Z, où fn = f(nTe), ce qui signifie que l'origine des t correspond à n = 0.
On cherche une fonction f*(t) qui soit "proche" de ce signal discret. Une idée consiste à prendre une fonction nulle en dehors des valeurs tn de l'échantillonnage, et valant fn pour t = tn, c'est-à-dire la fonction suivante :
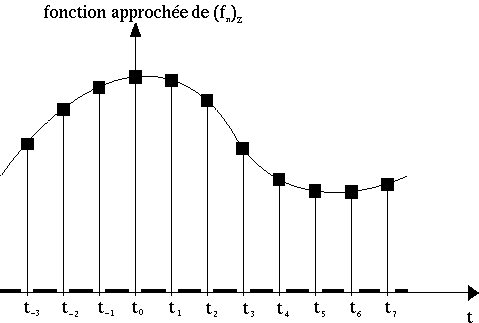
Cette fonction n'est malheureusement pas satisfaisante, car sa transformée de Fourier est la fonction nulle, ce qui est facile à vérifier. En revanche, si on définit f*(t) de la manière suivante :
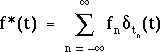
où ![]() désigne
l'impulsion de Dirac pour t = tn, on n'a plus le problème
précédent. Néanmoins, il ne faudra pas oublier que
f*(t) n'est pas une vraie fonction, mais une pseudo-fonction (ou "distribution"),
et qu'elle n'admet pas de transformée de Fourier, mais seulement
une "transformée de Fourier généralisée"
(on omettra, par la suite, l'adjectif "généralisée",
et on parlera de "transformée de Fourier").
désigne
l'impulsion de Dirac pour t = tn, on n'a plus le problème
précédent. Néanmoins, il ne faudra pas oublier que
f*(t) n'est pas une vraie fonction, mais une pseudo-fonction (ou "distribution"),
et qu'elle n'admet pas de transformée de Fourier, mais seulement
une "transformée de Fourier généralisée"
(on omettra, par la suite, l'adjectif "généralisée",
et on parlera de "transformée de Fourier").
En utilisant la formule (2.11) du chapitre 2, il est évident que :
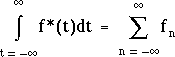
Par ailleurs, la même intégrale appliquée à f(t) peut être approximée ainsi :
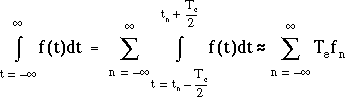
ce qui veut dire qu'on a l'approximation suivante :
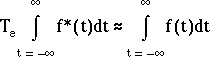
On peut se demander si, par analogie, l'approximation suivante ne serait pas également vraie :
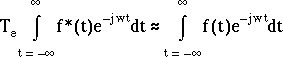
c'est-à-dire si la transformée de Fourier de f(t) ne serait
pas approximable par la "transformée de Fourier" de f*(t)
multipliée par Te.
Supposons que la fonction f(t) admette une transformée de Fourier
![]() .
La distribution f*(t) qui vient d'être introduite n'admet pas de
transformée de Fourier, mais elle admet une "transformée
de Fourier", que nous allons calculer.
.
La distribution f*(t) qui vient d'être introduite n'admet pas de
transformée de Fourier, mais elle admet une "transformée
de Fourier", que nous allons calculer.
L'implusion de Dirac ![]() vérifie,
par définition (voir chapitre 2) :
vérifie,
par définition (voir chapitre 2) :
![]()
En remplaçant t par -t dans cette égalité, on obtient :
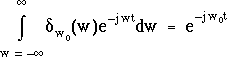 (3.1)
(3.1)
donc la "transformée de Fourier" de ![]() est
est
![]() ,
fonction de la famille de Fourier, qui est périodique.
,
fonction de la famille de Fourier, qui est périodique.
En utilisant la linéarité de la transformation de Fourier, on a donc :
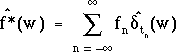
Or, d'après ce qu'on vient de voir, en inversant les variables muettes t et w :
![]()
donc :
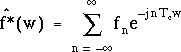 (3.2)
(3.2)
L'expression du second membre est ce qu'on appelle une série de Fourier.
Remarque :
La fonction ![]() vérifie
:
vérifie
:
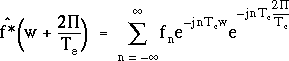
Or, comme ![]() ,
quel que soit l'entier relatif n, il en résulte que :
,
quel que soit l'entier relatif n, il en résulte que :
![]()
ce qui signifie que ![]() est
une fonction périodique, de période
est
une fonction périodique, de période ![]() .
Cela suffit d'ailleurs à prouver que
.
Cela suffit d'ailleurs à prouver que ![]() n'est
pas contenue dans T.
n'est
pas contenue dans T.
La "transformée de Fourier inverse" de la série
de Fourier ![]() est
très différente de la transformée de Fourier inverse
d'une fonction, telle qu'elle a été définie au chapitre
2. Au lieu d'associer une fonction f(t) à une fonction
est
très différente de la transformée de Fourier inverse
d'une fonction, telle qu'elle a été définie au chapitre
2. Au lieu d'associer une fonction f(t) à une fonction ![]() ,
elle associe à la série de Fourier
,
elle associe à la série de Fourier ![]() la
suite des coefficients fn de cette série de Fourier.
On demande ici au lecteur d'admettre la relation suivante, vraie pour un
entier relatif n quelconque :
la
suite des coefficients fn de cette série de Fourier.
On demande ici au lecteur d'admettre la relation suivante, vraie pour un
entier relatif n quelconque :
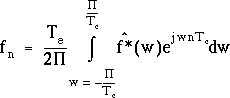 (3.3)
(3.3)
On va maintenant revenir à notre intuition initiale, selon laquelle il pourrait y avoir une relation entre les transformées de Fourier de f(t) et f*(t).
Appliquons d'abord la transformation de Fourier inverse à ![]() :
:
![]()
En particulier, si l'on remplace dans cette égalité t par tn = nTe :
![]()
A ce niveau du raisonnement, on utilise une astuce consistant à
découper R en une infinité d'intervalles du type ![]() ,
qui sont disjoints deux à deux si k est un entier relatif. L'égalité
précédente devient alors :
,
qui sont disjoints deux à deux si k est un entier relatif. L'égalité
précédente devient alors :
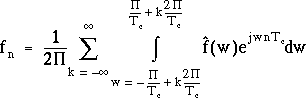
En faisant les changements de variables suivants :
![]()
il vient :
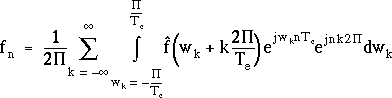
En remarquant que les facteurs ![]() sont
tous égaux à 1, et en remplaçant les variables muettes
wk par w, cette égalité devient :
sont
tous égaux à 1, et en remplaçant les variables muettes
wk par w, cette égalité devient :
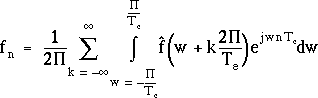 (3.4)
(3.4)
Si on intervertit la somme et l'intégrale du second membre, et qu'on égale les expressions de fn fournies par (3.3) et (3.4), on obtient l'égalité suivante :
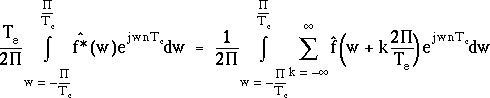
En identifiant les deux intégrandes, on établit l'égalité fondamentale suivante :
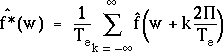 (3.5)
(3.5)
On a bien trouvé une relation entre les transformées de
Fourier de f(t) et f*(t), légèrement plus compliquée
que celle qu'on attendait. L'égalité (3.5), qui traduit cette
relation, signifie que ![]() est
égale à la somme de
est
égale à la somme de ![]() et
de toutes ses "translatées" de
et
de toutes ses "translatées" de ![]() ,
où k désigne un entier relatif quelconque.
,
où k désigne un entier relatif quelconque.
Remarque :
Soit une fonction f(t) admettant une transformée de Fourier,
et telle que la fonction ![]() soit
nulle en dehors d'un intervalle [wmin,wmax] de largeur
L, où L = wmax-wmin.
soit
nulle en dehors d'un intervalle [wmin,wmax] de largeur
L, où L = wmax-wmin.
Plutôt que de rester dans le cas général, et pour
mieux illustrer notre propos, prenons l'exemple de la fonction "sinus
cardinal", dont on a vu au chapitre 2 que sa transformée de
Fourier était égale, à un facteur ![]() près,
à la fonction "fenêtre", sauf aux deux points de
discontinuité de cette fonction :
près,
à la fonction "fenêtre", sauf aux deux points de
discontinuité de cette fonction :
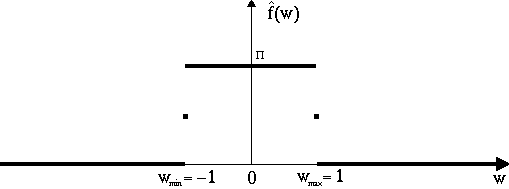
Pour la fonction ![]() ,
deux cas très différents se présentent :
,
deux cas très différents se présentent :
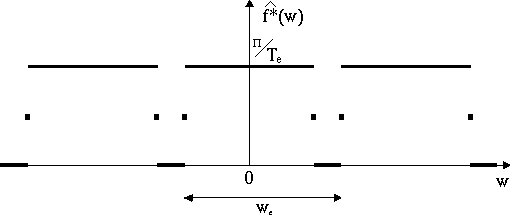
On peut retrouver la fonction ![]() à
partir de la fonction
à
partir de la fonction ![]() en
la "découpant" sur l'intervalle [wmin,wmax],
et en complétant ce "tronçon" par la valeur 0.
en
la "découpant" sur l'intervalle [wmin,wmax],
et en complétant ce "tronçon" par la valeur 0.
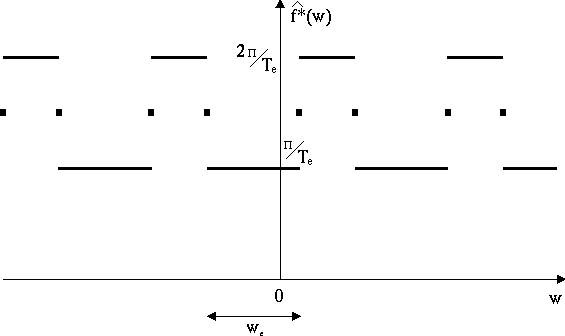
Dans ce cas, à cause du chevauchement des motifs, on ne peut
plus remonter de la fonction ![]() à
la fonction f(t).
à
la fonction f(t).
On peut généraliser ce résultat en énonçant le :
Théorème de Shannon :
La discrétisation d'un signal analogique f(t), dont le spectre
![]() est
nul en dehors d'un intervalle [wmin,wmax], fait perdre
de l'information si et seulement si la pulsation d'échantillonnage
we est strictement inférieure à la largeur du
spectre L = wmax-wmin.
est
nul en dehors d'un intervalle [wmin,wmax], fait perdre
de l'information si et seulement si la pulsation d'échantillonnage
we est strictement inférieure à la largeur du
spectre L = wmax-wmin.
Le théorème de Shannon a une application très importante dans le domaine du son, et plus précisément pour les enregistrements de disques compacts, sur lesquels le signal sonore est stocké de manière discrète. Pour qu'un lecteur de disques compacts puisse restituer le son analogique initial de manière satisfaisante, il faut éviter que la discrétisation de ce signal fasse perdre de l'information. Or, d'après le théorème de Shannon, la discrétisation d'un signal ne fait perdre d'information que si la pulsation d'échantillonnage we est strictement inférieure à la largeur du spectre L = wmax-wmin. Le signal qui provient d'un enregistrement sonore a-t-il un spectre de largeur finie ? En général non, mais comme l'oreille humaine n'est sensible qu'aux fréquences comprises dans l'intervalle [20 Hz,20000 Hz], on peut très bien se passer de tenir compte de la partie du spectre qui se trouve en dehors de cet intervalle audible. Voici donc les étapes permettant l'enregistrement des disques compacts sans perte d'information :
Désormais, nous savons qu'un signal contient la même information
sous forme discrète que sous forme analogique, pourvu que le critère
de Shannon ![]() soit
vérifié, avec L = wmax-wmin.
La transformation de Fourier discrète est censée être
l'équivalent, pour un signal discret, de la transformation de Fourier,
pour un signal analogique. C'est cette nouvelle transformation que nous
allons définir dans ce paragraphe.
soit
vérifié, avec L = wmax-wmin.
La transformation de Fourier discrète est censée être
l'équivalent, pour un signal discret, de la transformation de Fourier,
pour un signal analogique. C'est cette nouvelle transformation que nous
allons définir dans ce paragraphe.
Une même information est censée pouvoir être représentée par les quatre "objets" suivants :
Si les discrétisations sont faites de manière à respecter le critère de Shannon, ces quatre "objets" contiennent la même information. La question que nous nous posons maintenant est la suivante : sait-on passer de l'un quelconque de ces objets à un autre ? Remarquons d'abord qu'il existe douze transformations de ce genre, que l'on peut représenter par les relations suivantes :
1 -> 2 ; 1 -> 3 ; 1 -> 4 ; 3 -> 1 ; 3 -> 2 ; 3 -> 4 ;
2 -> 1 ; 2 -> 4 ; 2 -> 3 ; 4 -> 2 ; 4 -> 1 ; 4 -> 3.
Parmi ces douze transformations, nous en avons rencontré quatre jusqu'à présent, et ce sont ces quatre transformations qui apparaissent en rose. Faisons-en le détail :
Comme un spectre est une fonction complexe d'une variable réelle, on peut considérer un spectre comme un signal particulier et, de la même façon, on peut considérer un signal comme un spectre particulier, donc parmi les douze transformations citées précédemment, par cette simple symétrie, on sait en réaliser deux autres :
Enfin, en appliquant successivement deux des transformations déjà connues (il y en a six maintenant), on peut en réaliser quatre de plus :
Il ne reste donc plus que les deux transformations symétriques suivantes à réaliser :
3 -> 4 et 4 -> 3
Ces deux transformations sont les seules qui associent à un objet discret un autre objet discret, donc ce sont les seules qui pourront être utilisables par un calculateur discret. A l'aide du raisonnement précédent, qui consiste à "enchaîner" des transformations déjà connues, il semble que l'on puisse les réaliser toutes les deux :
Or, on commettrait une grave erreur dans le raisonnement en procédant de la sorte, erreur qui ne saute pas aux yeux, et que nous allons exposer dans le prochain sous-paragraphe.
Soit un signal analogique f(t), et ![]() son
spectre analogique. Soit we la pulsation d'échantillonnage
du signal, et wf la pulsation d'échantillonnage du spectre.
Si l'on veut que le signal discret et le spectre discret contiennent tous
deux la même information que le signal analogique (ou que le spectre
analogique), alors, d'après le théorème de Shannon
:
son
spectre analogique. Soit we la pulsation d'échantillonnage
du signal, et wf la pulsation d'échantillonnage du spectre.
Si l'on veut que le signal discret et le spectre discret contiennent tous
deux la même information que le signal analogique (ou que le spectre
analogique), alors, d'après le théorème de Shannon
:
Ceci implique en particulier que signal et spectre doivent tous deux avoir une largeur finie. Or, on peut montrer que ceci est impossible : il est impossible qu'un signal et son spectre soient simultanément de largeur finie. Par conséquent, il est impossible de discrétiser simultanément un signal et son spectre en respectant pour chacun d'eux le critère de Shannon. Ceci a la conséquence très importante suivante :
Le seul moyen pour qu'il existe simultanément deux transformations 3 -> 4 et 4 -> 3 inverses l'une de l'autre, est que ni l'objet 3 ni l'objet 4 ne contiennent toute l'information. Les deux transformations 3 -> 4 et 4 -> 3 inverses l'une de l'autre seront alors respectivement la transformation de Fourier discrète et la transformation de Fourier discrète inverse. Nous allons les définir dans le prochain paragraphe.
On appelle signal discret de longueur finie d'un signal analogique f(t), et on note (fn)[0,N-1], tout ensemble de N valeurs successives (N fini) provenant de l'échantillonnage de f(t) à une certaine pulsation we. Un signal discret de longueur finie est composé de valeurs fn qui forment un sous-ensemble des valeurs fn du signal discret (fn)Z. Alors que le signal discret (fn)Z peut contenir toute l'information du signal f(t), si we vérifie le critère de Shannon, un signal discret de longueur finie (fn)[0,N-1] ne peut bien sûr pas contenir toute cette information.
De la même façon, on appelle sous-spectre discret de
longueur finie, et on note ![]() [0,M-1],
tout ensemble de M valeurs successives (M fini) provenant de l'échantillonnage
de
[0,M-1],
tout ensemble de M valeurs successives (M fini) provenant de l'échantillonnage
de ![]() à
une certaine pulsation wf. Un spectre discret de longueur finie
est composé de valeurs
à
une certaine pulsation wf. Un spectre discret de longueur finie
est composé de valeurs ![]() qui
forment un sous-ensemble des valeurs
qui
forment un sous-ensemble des valeurs ![]() du spectre discret
du spectre discret ![]() Z.
Un spectre discret de longueur finie ne peut pas contenir, lui non plus,
toute l'information de départ.
Z.
Un spectre discret de longueur finie ne peut pas contenir, lui non plus,
toute l'information de départ.
C'est entre ces deux nouveaux objets que l'on va essayer de définir deux transformations inverses l'une de l'autre, que l'on appellera "transformation de Fourier discrète" et "transformation de Fourier discrète inverse". La raison en est double :
Pour obtenir un signal (ou un spectre) discret de longueur finie, deux cas se présentent :
Or on sait que, si un spectre analogique ![]() est
de largeur L finie, alors le signal analogique f(t) qui lui est associé
est forcément de largeur infinie, ce qui signifie que si un spectre
analogique rentre dans le cas 1, alors le signal analogique associé
rentre forcément dans le cas 2. C'est une situation de ce type que
nous allons détailler dans le paragraphe qui suit.
est
de largeur L finie, alors le signal analogique f(t) qui lui est associé
est forcément de largeur infinie, ce qui signifie que si un spectre
analogique rentre dans le cas 1, alors le signal analogique associé
rentre forcément dans le cas 2. C'est une situation de ce type que
nous allons détailler dans le paragraphe qui suit.
Soit f(t) un signal analogique, tel que le spectre ![]() soit
nul en dehors de l'intervalle [wmin,wmax], de largeur
L = wmax - wmin finie. On sait
que l'on peut discrétiser le signal f(t) de manière à
vérifier le critère de Shannon. Il suffit pour cela de choisir
la pulsation d'échantillonnage we supérieur ou
égal à L. Supposons par exemple que l'on choisisse we = L.
En revanche, on ne peut pas également vérifier le critère
de Shannon lors de la discrétisation du spectre. En conséquence,
comment choisir la pulsation d'échantillonnage du spectre wf
? C'est à cette question que nous allons tenter de répondre
dans ce paragraphe.
soit
nul en dehors de l'intervalle [wmin,wmax], de largeur
L = wmax - wmin finie. On sait
que l'on peut discrétiser le signal f(t) de manière à
vérifier le critère de Shannon. Il suffit pour cela de choisir
la pulsation d'échantillonnage we supérieur ou
égal à L. Supposons par exemple que l'on choisisse we = L.
En revanche, on ne peut pas également vérifier le critère
de Shannon lors de la discrétisation du spectre. En conséquence,
comment choisir la pulsation d'échantillonnage du spectre wf
? C'est à cette question que nous allons tenter de répondre
dans ce paragraphe.
Puisque le spectre rentre dans le cas 1 mentionné précédemment,
sa discrétisation à la pulsation d'échantillonnage
wf fournira ![]() valeurs
non nulles, qui constitueront un spectre discret de longueur
valeurs
non nulles, qui constitueront un spectre discret de longueur ![]() finie.
En revanche, comme le signal rentre dans le cas 2, il ne faudra conserver
que N valeurs successives parmi l'infinité de valeurs non nulles
fournies par la discrétisation à la pulsation d'échantillonnage
we = L, pour obtenir un signal discret de longueur
finie N. Comme on souhaite trouver une transformation inversible entre
ce spectre de longueur finie et un signal discret de longueur finie, il
faut nécessairement que l'un et l'autre contiennent la même
information, c'est-à-dire le même nombre de valeurs, donc
que :
finie.
En revanche, comme le signal rentre dans le cas 2, il ne faudra conserver
que N valeurs successives parmi l'infinité de valeurs non nulles
fournies par la discrétisation à la pulsation d'échantillonnage
we = L, pour obtenir un signal discret de longueur
finie N. Comme on souhaite trouver une transformation inversible entre
ce spectre de longueur finie et un signal discret de longueur finie, il
faut nécessairement que l'un et l'autre contiennent la même
information, c'est-à-dire le même nombre de valeurs, donc
que :
M = N (3.6)
En remplaçant M par ![]() ,
puis L par we, l'égalité (3.6) devient :
,
puis L par we, l'égalité (3.6) devient :
![]()
soit encore :
![]() (3.7)
(3.7)
Maintenant que les deux pulsations d'échantillonnage sont connues, nous allons chercher une transformation permettant de relier les N valeurs non nulles du spectre discret à N valeurs successives du signal discret.
Après discrétisation du spectre analogique à la
pulsation d'échantillonnage wf calculée précédemment,
on obtient un spectre discret ne comportant que N valeurs non nulles, que
l'on note ![]() [0,N-1].
Soit m un entier appartenant à l'intervalle [0,N-1]. On souhaiterait
pouvoir calculer
[0,N-1].
Soit m un entier appartenant à l'intervalle [0,N-1]. On souhaiterait
pouvoir calculer ![]() en
fonction de N valeurs successives du signal discret (fn)Z.
Est-ce possible ? C'est ce que nous allons voir dans ce paragraphe.
en
fonction de N valeurs successives du signal discret (fn)Z.
Est-ce possible ? C'est ce que nous allons voir dans ce paragraphe.
En partant de la définition de ![]() :
:
![]() (3.8)
(3.8)
Or, comme we vérifie par hypothèse le critère de Shannon, on sait que sur l'intervalle [wmin,wmax], d'après l'égalité (3.5) :
![]()
où f*(t) désigne la distribution introduite au paragraphe
II. Comme ![]() est
bien dans l'intervalle [wmin,wmax], ceci permet de
réécrire (3.8) sous la forme suivante :
est
bien dans l'intervalle [wmin,wmax], ceci permet de
réécrire (3.8) sous la forme suivante :
![]()
qui devient, d'après l'expression (3.2) de la "transformée de Fourier" de f*(t) :
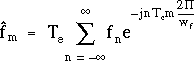
Cette expression se simplifie encore en remplaçant wf par son expression (3.7) :
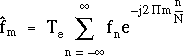 (3.9)
(3.9)
Il est clair qu'on ne peut pas exprimer ![]() en
fonction de N valeurs successives du signal discret (fn)Z,
puisque toutes ses valeurs (il y en a une infinité) interviennent
dans l'expression (3.9). En restreignant l'intervalle de variation de l'indice
n à [0,N-1] dans cette somme infinie, on n'a au mieux que l'approximation
suivante :
en
fonction de N valeurs successives du signal discret (fn)Z,
puisque toutes ses valeurs (il y en a une infinité) interviennent
dans l'expression (3.9). En restreignant l'intervalle de variation de l'indice
n à [0,N-1] dans cette somme infinie, on n'a au mieux que l'approximation
suivante :
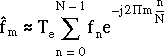 (3.10)
(3.10)
Nous pouvons maintenant donner la définition mathématique de la transformée de Fourier discrète, qui s'inspire fortement de (3.10).
On appelle transformation de Fourier discrète l'application qui, à un signal discret (fn)[0,N-1] de longueur N finie, associe la suite (Fm)[0,N-1] de N valeurs complexes, appelée transformée de Fourier discrète de (fn)[0,N-1], et définie par :
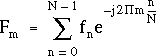 (3.11)
(3.11)
En comparant (3.11) à (3.10), on voit que Fm est une
approximation de ![]() ,
ce que l'on peut exprimer en disant que "la transformée de
Fourier discrète du signal discrétisé est une approximation
de la discrétisation de la transformée de Fourier du signal"
(au facteur Te près).
,
ce que l'on peut exprimer en disant que "la transformée de
Fourier discrète du signal discrétisé est une approximation
de la discrétisation de la transformée de Fourier du signal"
(au facteur Te près).
Comme on pouvait s'y attendre, cette transformation est inversible, et on demande au lecteur d'admettre que la transformation de Fourier discrète inverse associe à une suite (Fm)[0,N-1] de N valeurs complexes, la suite (fn)[0,N-1] de même longueur N, appelée transformée de Fourier discrète inverse de (Fm)[0,N-1], et définie par la relation suivante, inverse de (3.11) :
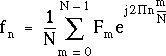 (3.12)
(3.12)
Remarque :
La transformation de Fourier discrète inverse ne diffère
de la transformation de Fourier discrète que par le signe de l'exponentielle
et le facteur ![]() .
.
Il nous reste maintenant à présenter un des algorithmes permettant le calcul de transformées de Fourier discrètes par ordinateur, ce qui était notre objectif initial. Cet algorithme est "l'algorithme de la transformation de Fourier rapide".
Pour calculer la transformée de Fourier discrète d'un signal discret (fn)[0,N-1] à l'aide de la formule (3.11), il semble que l'on ait à effectuer N multiplications pour chaque valeur Fm, c'est-à-dire N2 multiplications en tout. Pour une image numérique usuelle, de taille 256 x 256, cela fait 2564 multiplications, soit à peu près 4 milliards de multiplications ! Cette seule constatation démontre la nécessité de trouver un algorithme "rusé".
Il existe de nombreux algorithmes "rusés" permettant le calcul de la transformée de Fourier discrète d'un signal discret de longueur finie. Nous n'en présenterons qu'un, appelé "algorithme de la transformation de Fourier rapide" (TFR, ou FFT en anglais), dont la programmation en langage C sera effectuée lors des deux premières séances de travaux pratiques.
Dans l'égalité (3.11), le facteur suivant apparaît :
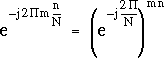
On note :
![]()
L'égalité (3.11) se réécrit donc :
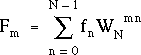 (3.13)
(3.13)
Remarques :
Exemple :
Si N = 8, alors :
![]()
Il existe de nombreuses redondances dans le calcul des différentes puissances de W8. En effet, on vérifie facilement que :
![]()
![]()
...
Il suffit de calculer les 8 premières puissances de W8 pour connaître toutes les puissances de W8 apparaissant dans (3.13).
Dans ce paragraphe, nous allons mener les calculs sous forme matricielle, ce qui nous permettra de leur donner une expression beaucoup plus compacte. Une telle écriture est possible si on remarque que, dans (3.13), les valeurs de la suite (Fm)[0,N-1] sont des combinaisons linéaires des valeurs de la suite (fn)[0,N-1], et que les coefficients de ces combinaisons linéaires sont des puissances du facteur de rotation WN. On peut donc réécrire (3.13) sous la forme matricielle suivante :
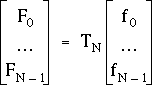 (3.14)
(3.14)
où TN désigne la matrice carrée, de taille N x N, dont l'élément courant vaut :
![]() (3.15)
(3.15)
si m désigne le numéro de ligne et n le numéro de colonne.
La matrice TN est facile à calculer grâce aux redondances citées précédemment, mais la multiplication matricielle (3.14) nécessite bien N2 multiplications, comme cela a déjà été mentionné.
L'algorithme de la transformation de Fourier rapide étant récursif, comme nous allons le voir, on a intérêt à choisir un nombre N qui soit une puissance de 2 :
N = 2P
C'est la raison pour laquelle les images numériques sont en général de taille 128 x 128 (128 = 27), 256 x 256 (256 = 28), 512 x 512 (512 = 29), ...
Dorénavant, nous fixons N à la valeur suivante :
N = 8 = 23
ce qui conduira à une profondeur de 3 dans la récursion. Par ailleurs, nous notons W le facteur de rotation W8.
Le fait de raisonner sur cette valeur particulière de N n'enlevera rien au caractère général de ce qui suit.
En découpant la matrice T8 en quatre quarts de taille 4 x 4, on peut calculer les valeurs de la suite (Fm)[0,7] en deux moitiés. Les quatre premières valeurs de cette suite sont données par :
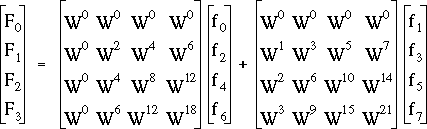 (3.16)
(3.16)
où W est une notation "allégée" pour W8.
A ce niveau du raisonnement, deux remarques très importantes (mais qui ne sautent pas forcément aux yeux !) doivent être faites :
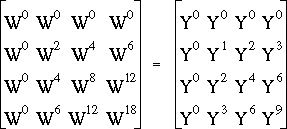
Comme, par ailleurs :
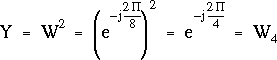
on constate, d'après (3.15), que cette matrice n'est autre que T4. Ainsi donc, on voit poindre le caractère récursif de ce calcul.
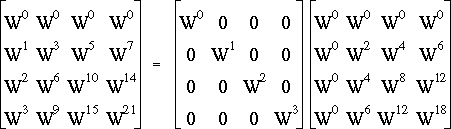
c'est-à-dire, d'après ce qu'on vient de montrer :
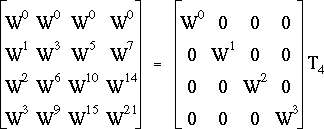
On peut donc réécrire (3.16) sous la forme suivante :
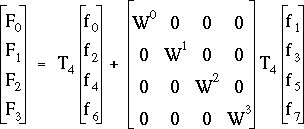 (3.17)
(3.17)
On demande au lecteur d'admettre que, par un calcul strictement similaire, on obtiendrait pour les quatre autres valeurs de la suite (Fm)[0,7] :
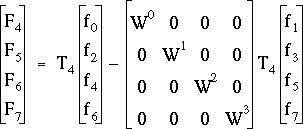 (3.18)
(3.18)
Le nombre de multiplications nécessaires pour calculer les expressions (3.17) et (3.18) vaut :
![]() (3.19)
(3.19)
qui apparaît deux fois ;
![]() (3.20)
(3.20)
qui apparaît deux fois ;
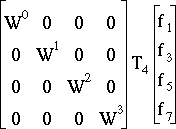
qui apparaît également deux fois.
On constate donc qu'au lieu des 64 multiplications annoncées, on n'en est déjà plus qu'à 36.
Les produits matriciels (3.19) et (3.20) peuvent être interprétés comme les calculs des transformées de Fourier discrètes des deux signaux discrets (f0,f2,f4,f6) et (f1,f3,f5,f7) de longueur 4 chacun, lesquelles transformées de Fourier discrètes peuvent être notées (Gm)[0,3] et (Hm)[0,3]. On peut donc appliquer à nouveau le raisonnement précédent, consistant à découper la matrice T4 en quatre quarts de taille 2 x 2. On obtient alors les écritures matricielles suivantes pour le calcul de la transformée de Fourier discrète (Gm)[0,3], par exemple :
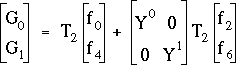
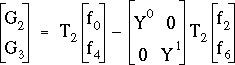
Les produits matriciels correspondant à des transformées de Fourier de signaux discrets de longueur 2 peuvent être aisément développés. Par exemple :
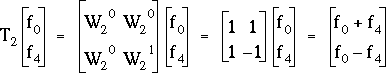
où on doit effectuer une addition et une soustraction, mais plus aucune multiplication. Or on sait que le temps de calcul d'une addition ou d'une soustraction est négligeable devant celui d'une multiplication.
Combien de multiplications faut-il faire au final ? Dénombrons-les :
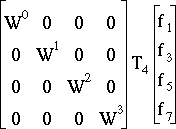
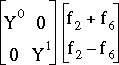
et 2 autres correspondant au produit :
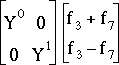
qui intervient dans le calcul de (Hm)[0,3].
On n'a donc plus que 8 multiplications à effectuer, au lieu des 64 prévues initialement !
De manière générale, quel est le nombre de multiplications nécessaires à l'algorithme que nous venons de décrire dans le cas particulier où N = 8, algorithme dit de la transformée de Fourier rapide ?
Supposons, comme nous l'avons préconisé plus haut, que
N = 2P. Le nombre d'étages de la récursion,
qui était 2 avec N = 8, vaut ![]() de
manière générale. A chaque étage, on peut montrer
que le nombre de multiplications est le même, et vaut
de
manière générale. A chaque étage, on peut montrer
que le nombre de multiplications est le même, et vaut ![]() .
Il y a donc en tout
.
Il y a donc en tout ![]() multiplications,
au lieu de N2.
multiplications,
au lieu de N2.
Exemple :
Pour une image 256 x 256, au lieu des 4 milliards de multiplications déjà mentionnés plus haut, il n'y en a plus que 400000 environ, c'est-à-dire 10000 fois moins ! Comprenez-vous pourquoi cet algorithme est appelé "algorithme de la transformation de Fourier rapide" ?
L'algorithme de la transformation de Fourier rapide peut être programmé de multiples façons, et nous allons en détailler une version particulière, appelée "algorithme papillon".
Reprenons le cas particulier d'un signal discret (fn)[0,7] de longueur N = 8. Dans l'algorithme de la transformation de Fourier rapide, il y aura trois niveaux de traitement des 8 valeurs de ce signal :
f0, f1, f2, f3, f4, f5, f6, f7
f0, f2, f4, f6, f1, f3, f5, f7
f0, f4, f2, f6, f1, f5, f3, f7
Comme on commence toujours une récursion par son dernier étage, c'est-à-dire par sa terminaison (se rappeler, par exemple, l'algorithme récursif du calcul de la factorielle), il faudra avant toute chose réordonner les valeurs du signal discret. Il existe un algorithme permettant de faire cela, et qui procède en trois étapes :
Pour convaincre le lecteur de la justesse de cet algorithme, appliquons-le sur un exemple :
Exemple :
Avec N = 8, donc P = 3, les trois étapes qui viennent d'être citées procèdent comme suit :
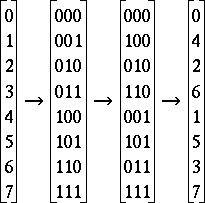
ce qui fournit bien l'ordre souhaité pour les indices.
On va à nouveau décrire ce qui se passe dans le cas particulier où N = 8, en supposant que les valeurs du signal discret ont été préalablement réordonnées grâce à l'algorithme qui vient d'être décrit. La suite du calcul peut en fait être résumée par un dessin, en convenant d'adopter les conventions suivantes :
Voici le dessin correspondant au cas N = 8 :
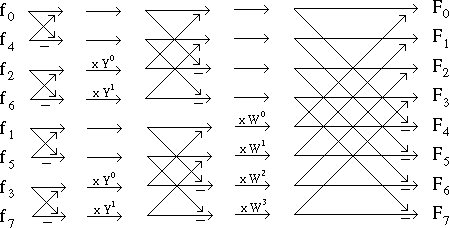
Remarques :
Il reste maintenant à convaincre le lecteur de l'intérêt de calculer des transformées de Fourier, discrètes ou non. Cela sera l'objet du quatrième et dernier chapitre de ce cours.