June 2020 - Nicolas Mellado

Persistence Analysis of Multi-scale Planar Structure Graph in Point Clouds

Thibault Lejemble (1), Claudio Mura (2), Loïc Barthe (1), Nicolas Mellado (1).
(1) CNRS, IRIT, Université de Toulouse, France.
(2) Department of Informatics, University of Zurich

Computer Graphics Forum (Eurographics 2020)

Preprint

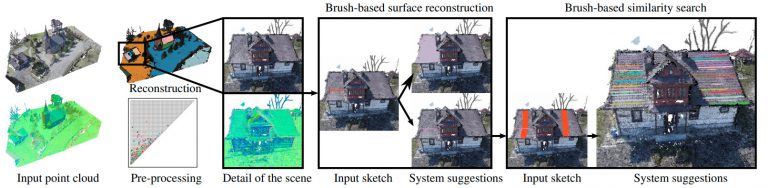
Modern acquisition techniques generate detailed point clouds that sample complex geometries. For instance, we are able to produce millimeter-scale acquisition of whole buildings. Processing and exploring geometrical information within such point clouds requires scalability, robustness to acquisition defects and the ability to model shapes at different scales. In this work, we propose a new representation that enriches point clouds with a multi-scale planar structure graph. We define the graph nodes as regions computed with planar segmentations at increasing scales and the graph edges connect regions that are similar across scales. Connected components of the graph define the planar structures present in the point cloud within a scale interval. For instance, with this information, any point is associated to one or several planar structures existing at different scales. We then use topological data analysis to filter the graph and provide the most prominent planar structures.

Our representation naturally encodes a large range of information. We show how to efficiently extract geometrical details (e.g. tiles of a roof), arrangements of simple shapes (e.g. steps and mean ramp of a staircase), and large-scale planar proxies (e.g. walls of a building) and present several interactive tools to visualize, select and reconstruct planar primitives directly from raw point clouds. The effectiveness of our approach is demonstrated by an extensive evaluation on a variety of input data, as well as by comparing against state-of-the-art techniques and by showing applications to polygonal mesh reconstruction.

Starting from an input point cloud equipped with normal vectors, our approach extracts meaningful planar components describing the geometry at multiple scales. Using persistence analysis, we offer to the user several ways to interactively explore, visualize and reconstruct the input data. The user can for instance generate planar reconstructions at arbitrary scales, select planar components by sketching directly on the point clouds, and/or find similar planar components.

Bibtex

@article{https://doi.org/10.1111/cgf.13910,
author = {Lejemble, T. and Mura, C. and Barthe, L. and Mellado, N.},
title = {Persistence Analysis of Multi-scale Planar Structure Graph in Point Clouds},
journal = {Computer Graphics Forum},
volume = {39},
number = {2},
pages = {35-50},
keywords = {CCS Concepts, • Computing methodologies → Point-based models; Shape analysis},
doi = {https://doi.org/10.1111/cgf.13910},
url = {https://onlinelibrary.wiley.com/doi/abs/10.1111/cgf.13910},
eprint = {https://onlinelibrary.wiley.com/doi/pdf/10.1111/cgf.13910},
year = {2020}
}